Lecture 2: Products
Check out the exercises for Lecture 2 (not included in the video lecture) at the end of this post. The rest of the post is mostly based on the video lecture.
2.1. The Big Secret
We ended last lecture saying that we should discuss examples of categories, as the next step. The two examples we had in mind had to do with the divisibility relation between numbers and composition of functions. Before discussing these examples, let us step back a bit and ask the question: what is the broad intuition behind the concept of a category -- what sort of phenomena of life/nature/science is it supposed to represent? Let us first answer this question for the concept of a directed graph. Directed graphs arise in life/nature/science as situations where a certain type of objects is identified and we would like to investigate a certain type of relation between these objects. For instance, the objects in question could be natural numbers (i.e., measures of whole quantities) and the relation we may be interested is the relation of one number dividing another number. We have already considered the associated directed graph, in the case when we limit to numbers 1,...,6, in the first lecture. In this example, there can only by at most one arrow between two vertices: there is an arrow when the source divides the target and, there is no arrow when this is not the case. Recall from the first lecture the picture illustrating this directed graph:
The reason why in this example there is at most one arrow between any two vertices is that we are concerned with only one type of relation (the divisibility relation). When we have more than one type of relation, multiple arrows may arise between two vertices -- each representing one of the considered types of relations. For instance, if along with divisibility we consider also the relation of "less than", we get two arrows from, say, 2 to 6 (because 2 divides 6 and at the same time, 2 is less than 6), while we only get one arrow from, say, 4 to 6 (because 4 does not divide 6, but 4 is less than 6). Allowing multiple arrows does not yet give us a category, though. In a category, we need to have, on top of that, composition: information of which third arrow does each pair of consecutive arrows give rise to. Say, for instance, two consecutive arrows "f" and "g" represent some relations: "f" is a relation relating object "A" with object "B", and "g" is a relation relating object "B" with object "C", as shown in the following diagram.
We can then ask the question: what conclusion can be drawn from these two relations? The answer to this question is what the composite of the two arrows, which is an arrow from "A" to "C" shown on the diagram above, represents. Thus, for example, consider the following instance of the diagram above:
As shown on this diagram, Peter is Mark's son and Mark is a brother of Tamar. These two relations, between Peter and Mark (the "son of" relation) and between Mark and Tamar (the "brother of" relation) together create some relation between Peter and Tamar, which answers the question "what conclusion can be drawn from these two relations?". The conclusion drawn here is that Peter is a nephew of Tamar. So we could set up a category where vertices are human beings and arrows are family relations between them, in which the composite of the "son of" relation and the "brother of" relation will be the "nephew of" relation. This simple example actually holds the big secret of category theory: if a directed graph can model phenomena consisting of objects and relations between them, then a category adds to this model the ability to reason -- to draw conclusions from compatible pairs of relations. This principle will actually prove to be the philosopher's stone when looking for examples of categories.
2.2. The Category of Natural Numbers
Let us now set up an example of a category where objects/vertices are all natural numbers (i.e., numbers 0,1,2,3,...) and arrows are given as suggested by the following picture, explained below.
This picture describes one of the arrows in the category we want to consider. an arrow from the object "6" to the object "3". The arrow is given by a way of arranging six apples into three boxes, as shown by the purple arrows between apples and boxes. In other words, the arrow is a mathematical function from a set having six members to a set having three members. Instead of thinking about apples and boxes, let us represent the members of the two sets by numbers 1 to 6 in the first case, and 1 to 3 in the second case. A function then must map every number from 1 to 6, to exactly one number from 1 to 3: in other words, back in the language of apples and boxes, every apple needs to be placed in exactly one box (well, we cannot place the same apple in two boxes anyway, but on top of that, we also do not want to leave any apples behind). Of course, what is shown on the picture is only one specific way of mapping numbers 1 to 6, to numbers 1 to 3. There are many others (there are other ways of arranging the same six apples into the three boxes). These other mappings also constitute arrows in the category we are busy building, and more generally, an arrow from an object "n" to an object "m" is given by a function mapping numbers 1 to n, to numbers 1 to m (in terms of apples and boxes, each arrow from "n" to "m" is given by one way of placing apples labeled 1 to n, inside boxes labeled 1 to m). Alert: one must not confuse here the arrow designating a function (like the arrow "f" displayed above with source "6" and target "3"), with the arrows describing individual mappings (the arrows shaped |--->) under a given function. So far, we have set up a directed graph, but not yet a category. We know what the vertices are (the numbers) as well as what the arrows are between every two vertices (the functions). Before describing composition (to turn this directed graph into a category), let us make one more remark about the arrows of our directed graph. Namely, we remark that each individual arrow in our directed graph can be wholly described by the effect of the corresponding function on each individual member in the domain of the function, and each of these effects can be represented using equalities such as those appearing at the bottom line of the diagram above, where "f" represents the function in question. For instance, the fourth equation,
tells us that the effect of the function "f" on the fourth member of the first set is the second member of the second set: the apple labeled "4" has been placed in the box labeled "2". These types of equations, which should be familiar to anyone who has worked with mathematical functions already at school, but especially in the first two years of an undergraduate mathematics course in e.g., calculus, will help us describe composition over our directed graph. A composition for our directed graph is given on the last line in the following figure, which gives a summary of the descriptions of objects and arrows as well:
Now that we know both axioms hold, we have a category! Yes, it took a while to build it, but please trust us that the experience gained will be useful in building other categories quicker.
As the purple equation suggest, in the category that we want to consider, a function "g" composed with a function "h" will be given by applying the function "h" first and then applying to the result the function "g". This is the usual notion of composition of functions, which we discussed also at the start of the first lecture. Let us, nevertheless, illustrate it in terms of apples and boxes... and trucks!
Here, "h" is an arrow from the vertex "2" to the vertex "3" (two random objects in our category, represented in the picture above as the set of two apples and the set of three boxes, respectively). The arrow "h" is a function given by a mapping of 1, 2 to 1, 2, 3, illustrated as a placement of apples labeled by 1, 2 into boxes labeled by 1, 2, 3. Look also at an alternative description of the same function "h" in terms of equations. The function "g" is an arrow in our category, from the vertex "3" to the vertex "2", which we now model as a placement of boxes into trucks. Namely, the first two boxes are placed in the first truck and the third box is placed in the second truck. The composite of these two arrows, which will be an arrow from the vertex "2" to the vertex "2", is given by the combined result of the placement of apples in boxes and the placement of boxes in trucks: the eventual placement of apples in the trucks! This is another good illustration of the "conclusion" we spoke earlier that the composite of two relations must describe; if I know how the apples were distributed in the boxes and I know how the boxes were distributed in the truck, then what conclusion will I be able to draw in terms of the relation between apples and trucks? The conclusion I will be able to draw is, of course, which apple ended up in which truck! Namely, in the scenario above, the first two apples ended up in the first truck and no apples in the second truck.
The arrangement of apples into trucks, which arises from the stated arrangement of apples into boxes and the stated arrangement of boxes into trucks, follows the equational rule defining composition of functions given earlier: to determine which truck a given apple "x" has ended up in, first look for the box in which "x" was placed (the box "h(x)") and then the truck in which that box was placed (the truck "g(h(x))") -- so the effect of the composite of "g" and "h" on "x" is given by "g(h(x))", as stated by the purple equation in the previous figure.
Now that we have described not only a directed graph, but also composition, we can claim that we have constructed a category. Alas, we must not forget about the axioms! Composition in a category cannot be just any way we like: it needs to adhere to the two axioms stated in the first lecture. To fulfill the first axiom, we need to check that the law
of associativity of composition holds for the composition that we have described above. Thinking of "h" as a placement of apples into boxes and "g" as a placement of boxes into trucks, we can think of "f" as a distribution of trucks to shops (for delivery of apples). The two sides of the equality above describe two different ways of arriving to the same conclusion. The left-hand side (LHS) first examines which apples were placed in which trucks, according to the intermediate step involving boxes (this is the "inner composite" in the expression, i.e., the composite of "g" and "h" inside the brackets), and then makes a conclusion about which apple went to which shop, by tracking the truck that carried that apple (this is the other composite, where "f" is composed with the result of composition of "g" and "h"). The right-hand side (RHS) of the same equality first makes a record of which box was carried to which shop (the inner composite in the RHS, of "f" and "g"), and then, based on this information and the information about which apples were placed in which boxes, makes a conclusion about the distribution of apples to the shops (the result of the inner composite composed with "h"). Now, obviously, which apple will end up in which shop, will be independent of these two methods of examination! If this elementary explanation is not good enough, and we want something more technical (but at the same time, more precise), we can use the equational presentation of the effect of a function on an member of its source set and compute the effect of both the LHS and the RHS function on a member "x":
Since in both cases we arrive to the same answer, we can conclude that the two triple-composite functions (the LHS and the RHS of the associativity equation) are the same function. If you want help with understanding the two sets of equalities above, please do make a request to explain this further in the comment section of this post.
Verification of the second axiom remains. According to the second axiom, each object "X" must have a special arrow looping in "X". This special arrow, written as "1" with subscript "X", needs to satisfy the equalities
for arbitrary arrows "g" and "f" (as long as the target of "g" is "X" and the source of "f" is "X", so that the composites in those equalities are allowed). So in our case, for each vertex, given by some number "X", we need to propose what the corresponding special arrow will be. As a looping arrow from "X" to "X", it needs to be a function mapping 1,...,X to 1,...,X. Let us consider the function that maps each number to itself: so 1 maps to 1, and 2 maps to 2, and 3 maps to 3, and so on. In the language of boxes, we can think of this as the action of not displacing the boxes: each box remains at its position. Then, composing this void action with some arrangement of apples in the boxes will give us back the same arrangement of apples in the boxes. Similarly, composing arrangement of boxes into trucks with the void action of not moving the boxes will result in the very same arrangement of boxes into trucks. These two facts explain the validity of the required equalities. Once again, we can establish the same equalities more formally, using the equational presentation of the effect of functions on members, keeping in mind that when the special arrow is applied to an input value, the output value will equal to the input value:
Now that we know both axioms hold, we have a category! Yes, it took a while to build it, but please trust us that the experience gained will be useful in building other categories quicker.
2.3. Counting Arrows
There is a reason why we want to put natural numbers in a category such as the one we created above. It will turn out that incorporation of functions between (finite) sets as relations between the quantities of those sets given by natural numbers, along with the above-described composition as a means of combining these relations, leads us to new insights about natural numbers. Revealing these insights is aided by first solving the following problem: how many arrows are there, in the category of natural numbers described above, from a vertex "a" to a vertex "b"?
Consider first an example where "a" is the number 4 and "b" is the number 3. An arrow from "4" to "3" is a function from a set with four members to a set with three members. To establish such a function, we need to choose for each of the four members of the first set, one of the three members of the second set. These choices are independent of each other. For the first member of the four-member set there are three choices. For the second member, again three, and so on. Since the choices are independent, we get altogether 3 times 3 times 3 times 3 many functions, i.e., there are that many arrows from "4" to "3".
The diagram above displays one of these arrows: the arrow, which, as a function, chooses the top-most member of the right set for the top-most member of the left set, the next member of the right set for the two next members of the left set, and the third member of the right set for the last member of the left set.
By a similar argument as above, we get that in general, the number of arrows from "a" to "b" is given by:
We will use this fact in what follows.
2.4. Compositional Insight to Multiplication of Natural Numbers
Now that we have set up the category of natural numbers, we want to apply it get some new insights about natural numbers. Elementary number theory is the branch of mathematics that studies natural numbers in terms of two basic operations: multiplication and addition of natural numbers. Addition of natural numbers arises as an abstraction of combining two quantities. Multiplication is more subtle. It can be defined in terms of addition, e.g., six times three is three plus three plus three, etc., six times, so 6x3=3+3+3+3+3+3=18. There is also a geometric interpretation of multiplication, related to its use for measuring area. Take a set with six members and a set with three members and create a new set in the shape of a grid whose rows are aligned with the six members of the first set and columns are aligned with the three members of the second set. This grid is shown in the following picture:
The number of vertices in the grid will of course be six times three, resulting from the required alignments (which will force the grid to be a 6 by 3 grid). The picture above shows much more than this grid -- let us explain the rest of the picture. Note that switching from the numbers 6 and 3 to sets having six and three members, respectively, ties well with how these numbers are viewed as objects in our category of natural numbers. We will now specify some arrows from this category. The alignment of rows of the grid with the six members of the first set can be seen as a function mapping each vertex in the grid to the member of the first set to which the row containing that vertex is aligned. So the three vertices in the bottom layer of the grid map to the bottom member of the left-hand side set in the picture (the set labeled "6"), the three vertices in the next layer map to the next member of that set, and so on. We thus get an arrow in the category of natural numbers, which we denote by a Greek letter with a subscript 1, as shown on the picture (note that this arrow has nothing to do with the number pi). This arrow has 18 as its source and 6 as its target. As a function, we can sort of think of it as projecting the grid onto its longer axis. Similarly, we have an arrow from "18" to "3", which performs the other projection: this time, vertices of the grid are mapped column-wise to the aligned members of the set with three members. We will shortly see that the top diagram of the picture, consisting of the two projection maps, exhibit a property describable purely in terms of composition in our category of natural numbers. This property will recognize the concept of multiplication. To identify the compositional property that will recognize multiplication, consider another ingredient of the picture above: another object of our category, the number "4", represented as a set of four points. For a moment, think of these four points as four consecutive instances of time. Then an arrow with source "4" and target "18" can be thought of as a particle moving around on the discrete grid of 18 vertices. We know well in physics that the movement of such particle can be uniquely described by the projections of this movement onto the axis of the grid. But projecting a location at a given time instance onto one of the axis is nothing other than the effect of composition of the function "h" describing the movement of the particle with the corresponding projection function. We get this way the functions "f" and "g", as shown on the picture, along with the following equalities:
These equalities can be confirmed on the picture by tracing along the corresponding mappings. For instance, to confirm the second equality, trace members of the bottom-most set, up along the yellow mapping, followed with tracing right-down along the dark purple mapping: the result should match with tracing the same members up-right along the blue mapping. Now the fact that the movement of the particle is uniquely determined by the effect of this movement on its projections onto the two axis illustrates a mathematical fact that in our category, the arrows "h" from "4" to "18" correspond in a one-to-one way with pairs of two arrows, where each pair consists of an arrow "f" from "4" to "6" and an arrow "g" from "4" to "3". This one-to-one correspondence guarantees that the number of arrows from "4" to "18" marches with the number of pairs of such arrows, which is given by the number of arrows from "4" to "6" multiplied by the number of arrows from "4" to "3". We get nothing other than an instance of a familiar law of multiplying numbers raised to the same power:
Of course, 18 is the only number that will satisfy this equality. So, we have been able to identify the object "18", which we created by multiplying 6 with 3, purely in terms of the language of the category: the object 18 is the unique object which admits arrows to 6 and 3, denoted by pi with subscript 1 and pi with subscript 2, respectively, such that for any other object (e.g., object 4) and any two arrows "f" and "g" from that other object to "6" and "3", respectively, there is exactly one arrow "h" from that other object to "18" satisfying the compositional equations displayed above. Equivalently, these equations describe a one-to-one correspondence between pairs of arrows "f" and "g", and arrows "h". Existence of such one-to-one correspondence defines the product 6x3. Of course, this story generalize to arbitrary numbers in the place of the numbers 6 and 3, resulting in the definition of a product of two numbers, purely in the language of the category of natural numbers. The fact that this definition is "purely in the language of the category" means that we could state such definition in a general category as well, to get a notion of multiplication of two objects in a category. This is what we will do in the next section. 2.5. The Notions of Product and Sum of Two Objects in a Category
Given two objects "A" and "B" in a category, their product is defined as a specific diagram
in the same category, such that for any extension of this diagram, there exists a unique filling arrow "h" as shown in
for which we would have
Equivalently stated, a product is an object "AxB" together with arrows as shown on the first diagram, such that for any object "C" there is a one-to-one correspondence between arrows "h" satisfying the compositional equations above and arbitrary pairs of arrows "f" and "g" with source "C" and target "A" and "B", respectively. This definition thus matches with how multiplication of two numbers was recognized in the category of natural numbers, which means that we have a general notion of a product of two objects in a category, which, in the special case, when the category is that of natural numbers, becomes precisely the notion of multiplication of natural numbers.When we are given a category, we can always consider the opposite, or the dual category. This is another category which has the same objects as the original category, the same arrows and composition, but with each arrow having the reverse direction in the new category. This also means that the composites would have to be written in reverse order. We could apply the notion of a product in the opposite category of a given category, to get a notion of what is known as a coproduct. Put simply, to obtain the definition of a coproduct, take the definition of a product and reverse the direction of all arrows in it, as suggested by the following sketch:
It would then be interesting to know what does this notion specialize to when considered in the category of natural numbers? Well, we can use the method of counting arrows to make a guess. The number of possible pairs of "f" and "g" is in this case C to raised to the power A, times C raised to the power B. The number of possible arrows "h" is C raised to the power the object "A?B", whatever that object is. These two numbers must match. So for instance, if as before, A=6, B=3 and C=4, the number "A?B" would be the value of the question mark that fits the following equation:There is of course unique such number: ?=6+3=9. So "A?B" must be the object "9" in the category of natural numbers, when A=6 and B=3. So... the coproduct "A?B" is the sum of A and B! This will be true not just for A=6 and B=3, but for any two natural number values of A and B. We arrive to a fascinating conclusion: not only the notion of addition of natural numbers is a particular instance of a category-theoretic notion of coproduct, but from the categorical perspective, addition of natural numbers is a dual construction to multiplication of natural numbers; to get one from the other, just reverse the direction of arrows in their category-theoretic description!
In general, the coproduct of two objects in any category is written as A+B and is often called a sum of objects, motivated from the particular case of the category of natural numbers. We have used the question mark above in the place of the plus symbol when we represented a coproduct as A?B, only so that we do not to spoil the surprise.
Note that while the notions of product and coproduct/sum are meaningful in any category, they do not always exist in every category. For instance, if we consider a portion of the category of natural numbers consisting of numbers less than, e.g., 10 (keeping arrows and composition unchanged), then in that category, not every two objects will have product or sum -- only those will have, for which the product/sum is less than 10.
2.6. Conclusion
In this lecture we first got a taste of how a category can be created out of familiar objects, on the example of natural numbers. This process required a non-trivial choice of arrows and composition to be included as part of the category. In particular, we turned the system of natural numbers into a category by choosing arrows to be functions between sets that represent the natural numbers as quantities. We could have created a category out of natural number in many other ways too (e.g., using the divisibility relation). What made this specific choice significant was that it led us to describing the notions of multiplication and addition of natural numbers in purely categorical terms, which allowed us to define product and sum of objects in an arbitrary category. Moreover, it turned out that the notions of product and sum so defined are "dual" notions to each other -- one can be obtained from the other by reversing the direction of arrows. This conceptual symmetry of arithmetic, a subject that is surely one of the oldest pieces of mathematics, could not have been discovered (and it indeed was not discovered) before categories came to existence. The notions of product and sum in a general category are actually useful notions for a large variety of many other examples of categories, not just the category of natural numbers. This type of phenomena, when a notion in a specific category is recognized to have a purely categorical description, which then leads to a general notion in a general category, and which applied to other specific categories recovers important notions encountered there, exists at almost every step in category theory. We already witnessed one illustration of such phenomenon: starting with multiplication of natural numbers, we designed a notion of product of two objects in a general category, and when applied to the dual category of the category of natural numbers, we remarkably obtained another important notion -- that of addition of natural numbers.
2.7. Exercises
Feel free to let us know of your attempts at the following exercises in the comments below.
Exercise 1. Answer the unanswered question suggested by Dr. Goswami: why is a number "n" raised to zero power equal to one, by interpreting this question as a question of counting arrows from the object "0" to the object "n" in the category of natural numbers.
Exercise 2. We did not quite show that addition of natural numbers satisfies the definition of a coproduct. What we showed rather is that if we assume that the coproduct exists, then the coproduct must be given by addition. In the case of multiplication, however, we showed the converse as well, that multiplication does indeed satisfy the categorical definition of a product. Indeed, recall that the definition of a product was extracted as an actual compositional feature of multiplication, using the large colorful diagram in Section 2.4. Draw a similar colorful diagram that would convince us that addition of natural numbers indeed has the compositional feature of the notion of coproduct.
Exercise 3. Another topic that was intended to be part of the lecture but was left out due to lack of time was application of the notions of product and coproduct to the category of natural numbers, where arrows are given by the divisibility relation. Show that in this category, categorical product of two numbers is their greatest common divisor and coproduct is... (complete the sentence).








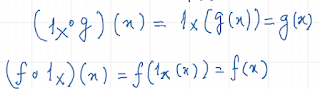











Comments
Post a Comment